Dimensional deconstruction

In theoretical physics, dimensional deconstruction is a method to construct d-dimensional theories that behave as higher-dimensional theories in a certain range of energies. The resulting theory is a gauge theory whose gauge group is a direct product of many copies of the same group; each copy may be interpreted as the gauge group located at a particular point along a new, discrete, "deconstructed" (d+1)st dimension. The spectrum of matter fields is a set of bifundamental representations expressed by a quiver diagram that is analogous to lattices in lattice gauge theory.

"Deconstruction" in physics was introduced by Nima Arkani-Hamed, Andy Cohen and Howard Georgi, and independently by Christopher T. Hill, Stefan Pokorski and Jing Wang. The latter authors viewed the method as a lattice approximation to the real space of extra dimensions, while maintaining the full gauge symmetries to obtain the low energy effective description of the physics. This leads to a rationale for extensions of the Standard Model based upon product gauge groups, 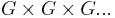G\times G\times G ..., such as anticipated in "topcolor" models of electroweak symmetry breaking.

The little Higgs theories are also examples of phenomenologically interesting theories inspired by deconstruction.

References

External links